sounds like a nice thing to think about in a coffee break:
pitch shifting with "real" instruments and vocals is a bit of a complex problem to make it sound good [1], but yes, a special kind of resampling is probably what you're after.
I can achieve an octave of the signal multiplying it by itself (doubling the frequencies).Is that true? I can see that for a single tone, because for an input signal
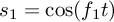 you'd get
you'd get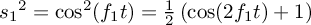 ,
, but for a musical instrument, you'd typically have at least two tones making up the timbre:
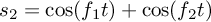 , so
, so 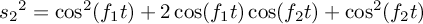 , of
which we know the form of the first and last, term, yielding
, of
which we know the form of the first and last, term, yielding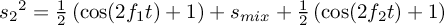 , with
, with 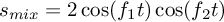 .
.Now,
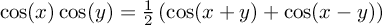 , which means that
the signal
, which means that
the signal 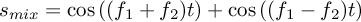 , containing both first intermodulations of
, containing both first intermodulations of 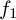 and
and 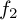 , i.e.
, i.e.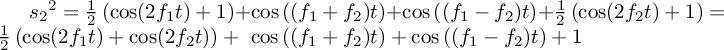
which means the resulting signal would have four times as much energy at the "unwanted" intermodulations than at twice the input frequencies, which is especially problematic since
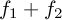 will
probably be somewhere between
will
probably be somewhere between 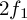 and
and 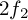 , and
hence can't be filtered out (like the DC component
, and
hence can't be filtered out (like the DC component 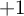 ).
).So, yes, intuitively, going through frequency domain does sound good:
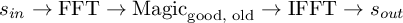
However, we know that the Magic used here cannot be linear, because multiplication with something in frequency domain is equal to convolution with its time domain equivalent, and convolution is linear, and linear operations don't shift frequencies individually by different amounts (e.g.
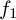 needs to
be shifted by
needs to
be shifted by 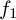 , unlike
, unlike 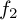 , which
needs to be shifted by
, which
needs to be shifted by 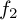 ). One
way would be to interpolate in frequency domain (notice that the
interleaver at the right top is de facto a simple interpolator):
). One
way would be to interpolate in frequency domain (notice that the
interleaver at the right top is de facto a simple interpolator):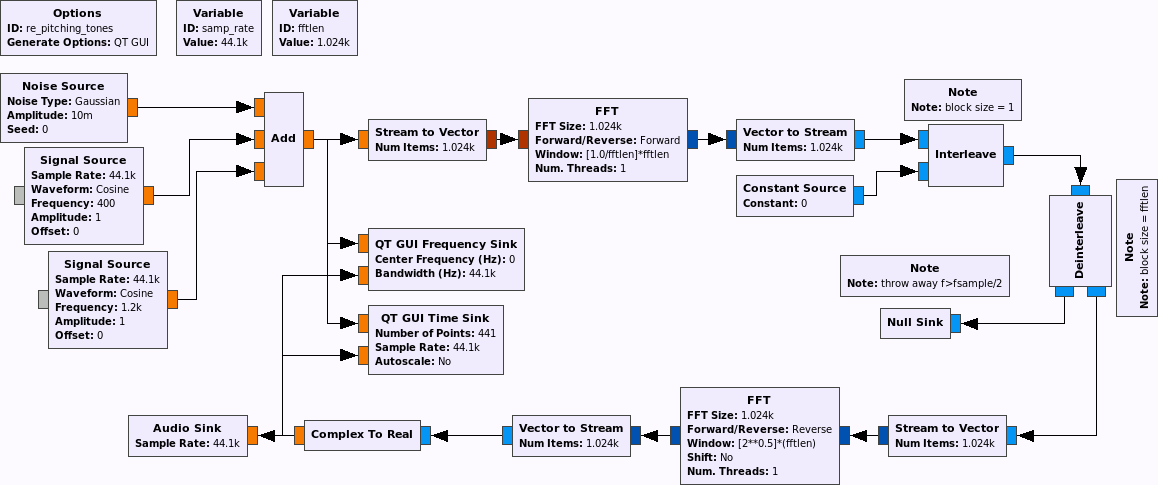
The resulting signals would behave like this (top time, bottom frequency domain of in- and output)
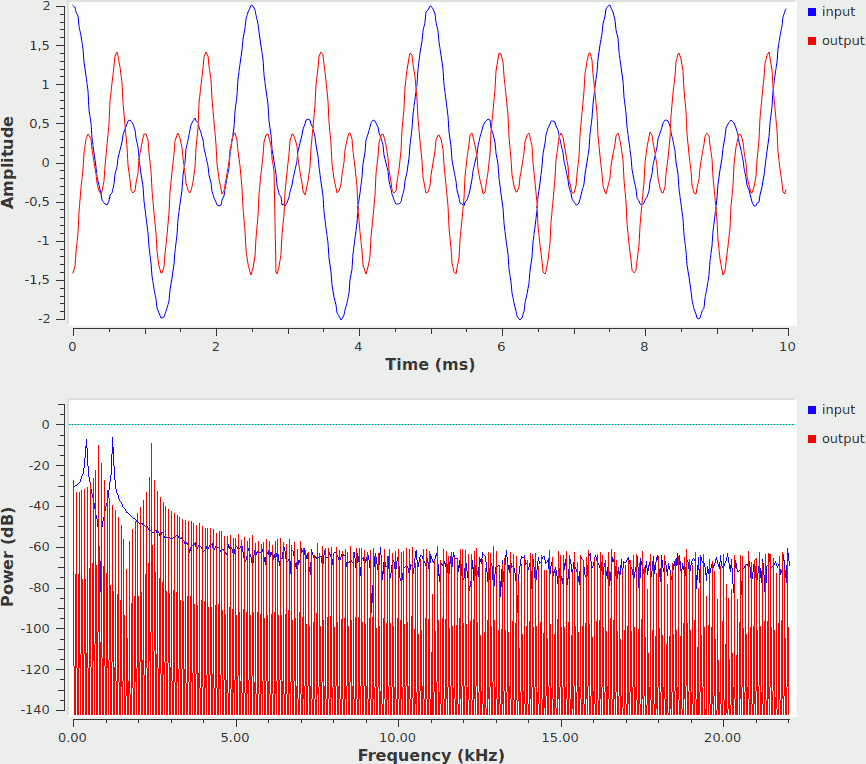
Notice a few things:
The FFT/IFFT + interleaver is not doing any filtering, and that's what you see as jagged discontinuity in the signal spectrum. I don't think this is going to sound overly nice with "real" sounds, but it might "do the job"; you know these "springy" sounds you get when your GSM connection is really bad. That.
On the other hand, doing filtering in frequency domain (as in "using a proper interpolator rather than just inserting zeros") will have side effects on the time domain signal, and render it pretty unusuable (multiplication with the repeated inverse fourier transform of the filter response...).
I'm really no expert in Audio processing, but I guess there's more to this problem than basic operations.
Best regards,
Marcus
[1] I wrote something completely "out of the blue". It has to do with goats. Which is not my fault. But I found it funny enough to write an answer.
http://dsp.stackexchange.com/questions/28356/convert-one-sound-sample-in-different-sample-where-each-samples-pitch-is-a-note/28362#28362
On 13.03.2016 13:29, Murray Thomson
wrote:
MurrayThanks,I would appreciate if someone can suggest the best way to go or point me in the right direction.I can achieve an octave of the signal multiplying it by itself (doubling the frequencies). I thought I could do this resampling the signal but now I'm not too sure. Do I need to use an FFT block for this?Hi,This is probably an easy one but I'm stuck and i could do with some help. My goal is to get a musical note from the microphone and shift its frequency to transform the note to a different scale. For this to happen, I need to multiply all the frequencies for e.g. 1.5.
_______________________________________________ Discuss-gnuradio mailing list address@hidden https://lists.gnu.org/mailman/listinfo/discuss-gnuradio