So correlating is digitally mixing something with a predetermined sequence?um, no. Not in the sense that I'd use "correlating".
Mixing in this context is simple point-wise multiplication.
I guess, then, if you have a PSK waveform you might multiply it by something, starting at various offsets in the signal, to try and decode it?A correlation of two digital signals is pretty much that, you take the first signal, multiply it with the second, sum that up, and then shift either signal, rinse, repeat. You get a vector of correlation coefficients which can be interpreted as "how similar is the first signal to the second being shifted by a different sample delays".
Generally, if you have a known pulse shape (i.e. your transmitter takes the transmit symbol, in case of BPSK that would be either +1 or -1, and multiplies it with the pulse shape) you can correlate against that pulse shape, and you'll get the factor with which the pulse was multiplied (which is your transmit symbol combined with whatever your channel does to the signal).
Because we were talking about the DFT/FFT:
Look up the Discrete Fourier Transform in its Matrix form: You take a vector of samples
 and
multiply it with a matrix
and
multiply it with a matrix 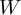 to get the
discrete Fourier transform of
to get the
discrete Fourier transform of  , which I
shall denote
, which I
shall denote 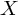 :
: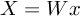 , with
, with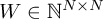 (i.e. a square matrix, representing the N-point
DFT)
(i.e. a square matrix, representing the N-point
DFT)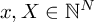 (i.e. column vectors).
(i.e. column vectors).Remember how you do matrix-vector multiplication:
To get the result's element in its
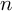 -th
result row and the
-th
result row and the 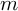 -th result
column, you take row
-th result
column, you take row 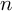 from the
left factor (i.e. a row of
from the
left factor (i.e. a row of 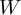 , which has
, which has
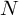 rows, so
rows, so 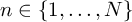 ), and multiply it point-wise with
), and multiply it point-wise with 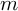 -th column
of the right factor (
-th column
of the right factor ( , which only
has 1 column, so
, which only
has 1 column, so  )
and calculate the sum.
)
and calculate the sum.Now, point-wise multiplication & summation is what is defined as dot product, so what happens here is that you take your sample vector
 and
calculate the dot products with each row of the DFT Matrix
and
calculate the dot products with each row of the DFT Matrix 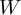 . The rows
of the DFT matrices happen to be nothing else but samples of complex
sinusoids.
. The rows
of the DFT matrices happen to be nothing else but samples of complex
sinusoids.Regarding Lou's:
The FFT is different (I actually don't know how it works, other than it operates on 2^n samples), but the output is the same.Exactly, an FFT is just a specific implementation of the DFT (because you really don't want to do vector-matrix multiplication if you can avoid it, because you'd end up doing
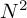 multiplications and summations), and is mathematically equivalent.
In a first step, the fact that the DFT matrix is pretty regular and
all entries appear twice is used to save calculations. Modern FFTs
do all kind of cool optimizations that I don't understand the least,
but what I learnt is that today, the Radix-2 algorithm isn't the
only FFT algorithm in existence, and so it turns out that for
example the FFTW library, which GNU Radio uses to do its FFTs, can
deal with any DFT that has a prime factorization with "nearly no"
prime factors >7 [1].
multiplications and summations), and is mathematically equivalent.
In a first step, the fact that the DFT matrix is pretty regular and
all entries appear twice is used to save calculations. Modern FFTs
do all kind of cool optimizations that I don't understand the least,
but what I learnt is that today, the Radix-2 algorithm isn't the
only FFT algorithm in existence, and so it turns out that for
example the FFTW library, which GNU Radio uses to do its FFTs, can
deal with any DFT that has a prime factorization with "nearly no"
prime factors >7 [1].So, yeah, DSP often gets a lot easier if you just consider it an exercise in linear algebra :)
Cheers,
Marcus
[1] http://www.fftw.org/doc/Complex-DFTs.html#Complex-DFTs
On 20.03.2016 17:45, Henry Barton
wrote:
So correlating is digitally mixing something with a predetermined sequence? I’ve been struggling to figure out what correlation means and this seems right. I guess, then, if you have a PSK waveform you might multiply it by something, starting at various offsets in the signal, to try and decode it?
Sent from Windows Mail
Yes, pretty much. With the DFT (and the continuous one) you are correlating
the input waveform with harmonically related, complex sinusoids; essentially
for each harmonic you mix it down to DC then sum (integrate). The FFT is
different (I actually don't know how it works, other than it operates on 2^n
samples), but the output is the same.
Lou
Henry Barton wrote
> I’ve read up on the FFT and DSP and I must say I’m impressed that
> multiplying two waveforms is the digital equivalent of heterodyning. Am I
> right in my understanding that finding frequency components (FFT-ing) is
> simply multiplying a series of known sine waves by your input waveform?
--
View this message in context: http://gnuradio.4.n7.nabble.com/Handling-of-IQ-files-tp58915p58935.html
Sent from the GnuRadio mailing list archive at Nabble.com.
_______________________________________________
Discuss-gnuradio mailing list
address@hidden
https://lists.gnu.org/mailman/listinfo/discuss-gnuradio
_______________________________________________ Discuss-gnuradio mailing list address@hidden https://lists.gnu.org/mailman/listinfo/discuss-gnuradio