Hi Fons,
On 10/26/2016 10:26 PM, Fons Adriaensen
wrote:
No! My point is that the accuracy of the clock used for the timestamps is much lower than the quality of the sample clocks involved.On Wed, Oct 26, 2016 at 01:30:19PM +0200, Marcus Müller wrote:Now, these microsecond timestamps will introduce a /third/ clock into our problems. I can see how the control loop converges in case of that clock being both faster than your sampling clock and relatively well-behaved, but: is this an assumption we can generally make?If I understand this correctly, you say that the resolution of the timer should be better than the sample time ?
Hm, interesting point.This is not required. The timer is read whenever a _block_ of samples is handled at either side. For audio a typical block size is 256 samples, 5.333 ms at 48 kHz, or more than 5000 clock ticks. Round-off error is small compared to timing jitter, and will be filtered by the DLL anyway.
That means that you say that your CPU clock-based timing estimator is unbiased; if I'm not mistaken by my understanding right now (and I did have a beer just now), that'll require a higher-order control loop if the clocks drift, which they will inevitably do.It doesn't have any cumulative effect.
You don't happen to have an estimate for CPU clock stability?
Exactly; that what was I was worried about. I don't have any data on the frequency stability of PC clocks – but I'm 100% sure a USRP's oscillator should be betterThe actual frequency of the clock used to measure time doesn't matter as long as it has reasonable short term stability (and both sides use the same clock of course).
Hm, at 100MS/s, the integration periods to get stable rate estimates relative to CPU clock would probably get pretty long, sample-wise, wouldn't they? In other words, while we still need to aggregate samples to get a block of samples temporally long enough for the CPU time estimate to be stable, buffers are already flowing over. Also, I'm still confused: Let's say we have two rates that we need to match,Let's first just focus on the Audio part (I personally think matching a 100MS/s2ppm stream to a whatever 31.42MS/s
20ppb stream with a clock that has microsecond resolution and more ppms is out of question):
No, it would be possible, there is no need to time individual samples.
 and
and 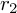 , with
, with 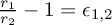 for pretty small values of
for pretty small values of  , i.e. relatively well matched. If we now use a third rate,
, i.e. relatively well matched. If we now use a third rate, 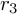 (namely, the clock resolution of the PC), whose
(namely, the clock resolution of the PC), whose 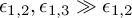 , how does that work out? I feel like that will add more jitter, mathematically?
, how does that work out? I feel like that will add more jitter, mathematically?
Not really, there's no direct triggering. Basically, a source block gets initially called to fill its output buffer. It decides autonomously how much samples it wants to put in there, and returns. The change in input buffer(==source output buffer) fillage causes the downstream block to be called (as long as that has enough space in its output buffer), and that block autonomously decides how much of the samples available it wants to consume. The remainder remains in the input buffer and the next source output will be appended to that. The source, in the meantime (all blocks run in separate threads) might have been called again, or will be called after this move made space in its output buffer, again, and adds samples to its output buffer. For example, a fictive source always produces 1200 samples at once, or multiples of that. A fictive downstream block can consume any number of samples per iteration <= 1000. So, at first, all buffers are empty, the source produces 1200, is called immediately again (since there's space for let's say 4096 samples in the buffer), and takes its time to produce the next 1200 samples. In the meantime, the downstream block is called, and after a short time consumes 1000 of the 1200 samples, and 200 unprocessed samples stay. During that processing, the source finishes its second iteration, leading to 1400 samples in the buffer after the moment the downstream block finishes its first iteration. This time, the operation doesn't take as long (for whatever reason – maybe there's more CPU available now), so even before the source finishes its third iteration, the downstream block finishes, so there's only 400 samples left. It immediately gets called again, processing all 400 samples. In this scenario, there's blocks of 1000, 1000, 400 samples being processed. In reality, the sizes often vary very much more in more-than-two-block flow graphs :)Hm, OK. So you get atime estimate. Wow! Third loop of control!
Yes, there are three loops: a DLL on either side, and control loop that drives the resampler. But they are not nested, so this won't affect stability. In theory all filtering could be done by the latter loop, and the DLLs would not be necessary. But there are practical reasons for having them: - it provides a layer of abstraction, which - simplifies the design of the resampling control loop, - simplifies error detection and graceful recovery.Do you have any ressources on that? How is that cycle start time prediction (which is a sampling rate estimator, inherently) realized?in pseudo-C: while (true) { wait_for_start_of_next_period(); er = time_now() - t1; t0 = t1 t1 += dt + w1 * er; dt += w2 * er; } where t0 = filtered start time of current period (= previous t1) t1 = predicted start time of next period dt = current estimate of period time. w1, w2 = filter coefficients. wait_for_start_of_next_period() is a call the the sound card driver. It returns when there is a full buffer of samples available to be read and written. On some systems you don't have the loop and wait() but provide a callback instead. The code above assumes a constant number of samples per iteration. If that's not the case things get a little more complicated - the actual number of samples in each block needs to be taken into account - but not fundamentally different.I think it'll be a little unlikely to implement this as a block that you drop in somewhere in your flow graph.In theory it would be possible. The requirement then (assuming RF in and audio out) is that everything upstream is directly or indirectly triggered by the RF clock, and everything downstream by the audio clock. Don't know if that's possible in GR (still have to discover the internals).
Yeah, there's a lot of uncertainty of how much time will pass between the audio sink consumes a block of samples and an upstream block being called again.it has to be done directly inside the audio sink.That would probably be the best solution. So you'd have fixed decimation block somewhere, producing a nominal audio sample rate, and the sink takes care of resampling that to the actual one.
But that assumption fails with GNU Radio in general! There's always faster and slower blocks. The input buffer of the slower block, even in a signal processing chain that is faster than the sampling rate of the source block, should be fuller on average (unless every single block's processing time is sufficiently shorter than the production of a sample packet by the source. In general, GNU Radio does kind of benefit from and foster fuller buffers, because many algorithms are more efficient on larger sample blocks).The reason simply is that unlike audio architectures, and especially the low-latency Jack arch, GNU Radio doesn't depend on fixed sample packet sizes, and as an effect of that, you're very likely to see very jumpy throughput scenarios.The only assumption for this to work is that there is no 'chocking point', i.e. all modules are fast enough to keep up with the signal.
... and we're back at the question of how much we can trust the CPU clock as a base for estimating latencies :)Then what matters is how over how much time the stream of sample blocks delivered to the resampler must be observed to get a reliable estimate of the average sample rate. The most important parameter if blocks have variable size and irregular timing is the maximim time between two blocks. This will determine both the amount of buffering required and the DLL loop bandwidth.
The problem gets even worse if the output buffer of the rate-correction block isn't directly coupled to the consuming (audio) clock – if there's nondeterministic error introduced at theestimation, the control loop Fons showed is likely to break down at some point.
Not if things are correctly dimensioned. The whole control system is symmetric w.r.t. the two sides.
+ third side, time as reported by OS is jittery, too, and my hypothesis is that it's much more jittery than the sample clocksIf it can tolerate jitter from both sides.
That is a very good analogy!But normally one end will be close to the audio HW. The only consequence of having no direct coupling is that the _average_ error resulting from this is not corrected. This only means you don't have defined latency.So in this case, the throughput-optimizing architecture of GNU Radio is in conflict with the wish for good delay estimatorNot having constant-rate and constant-size blocks does not fundamentally change anything. The variability just must be taken into account when dimensioning the buffers and loops. You get the same situation when one side is not some local hardware but e.g. a network stream.
Good point. But maybe I'm not fully understanding your control scheme: How does your system combat random jitter of time_now()? Best regards, MarcusIn practice, the "best" clock in most GNU Radio flow graphs attached to an SDR receiver is the clock of the SDR receiver (RTL dongles notwithstanding); if we had a way of measuring other clocks, especially CPU time and audio time, using the sample rate coming out of these devices, that'd be rather handy for all kinds of open-loop resampling.Open loop doesn't work. No matter how accurate your frequency ratio estimation, any remaining error is integrated. You need _some_ form of feedback to avoid that. Which will lead you back to something similar to the presented scheme.
Ciao,